Rumus – rumus matematika
- Volume balok
V = panjang x lebar x tinggi
= p x l x t
CONTOH SOAL :
Hitung Volum balok dengan ukuran 6 cm x 5 cm x 4 cm !
Jawaban :
Dik : p = 6 cm
L = 5 cm
t = 4 cm
dit : Volume:
V = p x l x t
= 6 cm x 5 cm x 4 cm
= 120 cm
- 2. Rumus Persamaan Kuadrat
Bentuk umum persamaan kuadrat adalah :
ax2 + bx + c = 0 0¹, a
ax2 + bx + c = 0 0¹, a
Untuk mendapatkan akar persamaan kuadrat dapat dilakukan dengan tiga cara, yaitu: pemfaktoran, melengkapkan kuadrat, dan rumus abc.
CONTOH SOAL :
Carilah akar persamaan kuadrat x2 – 4x – 5 = 0.
Penyelesaian :
a. Cara pemfaktoran :
x2 – 4x – 5 = 0
(x – 5)(x + 1) = 0
Diperoleh x1 = 5 atau x2 = -1.
b. Cara melengkapkan kuadrat :
x2 – 4x – 5 = 0
x2 – 4x + 22 – 22 – 5 = 0
(x – 2)2 – 9 = 0
(x – 2)2 = 9
x – 2 3±=
3±x = 2
Diperoleh x1 = 2 + 3 = 5 atau x2 = 2 – 3 = -1.
c. Dengan rumus abc, yaitu :
x2 – 4x – 5 = 0
a = 1, b = -4, dan c = -5
= = 3±= 2
Diperoleh x1 = 2 + 3 = 5 atau x2 = 2 – 3 = -1.
Penyelesaian :
a. Cara pemfaktoran :
x2 – 4x – 5 = 0
(x – 5)(x + 1) = 0
Diperoleh x1 = 5 atau x2 = -1.
b. Cara melengkapkan kuadrat :
x2 – 4x – 5 = 0
x2 – 4x + 22 – 22 – 5 = 0
(x – 2)2 – 9 = 0
(x – 2)2 = 9
x – 2 3±=
3±x = 2
Diperoleh x1 = 2 + 3 = 5 atau x2 = 2 – 3 = -1.
c. Dengan rumus abc, yaitu :
x2 – 4x – 5 = 0
a = 1, b = -4, dan c = -5
= = 3±= 2
Diperoleh x1 = 2 + 3 = 5 atau x2 = 2 – 3 = -1.
1. 3.Rumus Kerucut
- Luas : (phi . r) . (S . r)
- S : Sisi miring kerucut dari alas ke puncak (bukan tingi)
- Luas : (phi . r) . (S . r)
- S : Sisi miring kerucut dari alas ke puncak (bukan tingi)
CONTOH SOAL :
Luas sebuah kerucut 990 cm2,dan jari-jarinya 21cm, jika phi=22/7,berapakah panjang sisi miring dari kerucut tersebut..?
Jawab:
panjang sisi miring = luas/phi.r2
= 990/22/7.21
= 990/66
= 15 cm.
4.Penyelesaian SPLK implisit yang dapat difaktorkan adalah sebagai berikut.
- Ubah persamaan ax2 + by2 + cxy + dx + ey + f = 0 menjadi bentuk (mx + ny)2 - s2 = 0 selanjutnya diubah menjadi {(mx + ny) + s}{(mx + ny) -s} = 0, sehingga diperoleh
mx + ny + s = 0 atau mx + ny -s = 0 - Eliminasikan persamaan px + qy + r = 0 dengan mx + ny + s = 0 dan mx + ny -s = 0 sehingga diperolah nilai x dan y.
Contoh
Tentukan himpunan penyelesaian SPLK x2 - 6xy + 9y2 - 36 = 0
Tentukan himpunan penyelesaian SPLK x2 - 6xy + 9y2 - 36 = 0
Jawab:
x2 - 6xy + 9y2 - 36 = 0
 (x - 3y)2 - 36 = 0
(x - 3y)2 - 36 = 0
 (x - 3y + 6)(x - 3y - 6) = 0
(x - 3y + 6)(x - 3y - 6) = 0
 x - 3y + 6 = 0 atau x - 3y - 6 = 0
x - 3y + 6 = 0 atau x - 3y - 6 = 0
 x - 3y = -6 atau x - 3y = 6
x - 3y = -6 atau x - 3y = 6
Eliminasikan x + y = 2 dengan x - 3y = -6 dan x - 3y = 6
x2 - 6xy + 9y2 - 36 = 0
Eliminasikan x + y = 2 dengan x - 3y = -6 dan x - 3y = 6
x + y = 2
x - 3y = -6
4y = 8 x + 2 = 8
y = 2 x = 0
x + y = 2
x - 3y = -6
4y = 8 x + 2 = 8
y = 2 x = 0
5.Tiga Vektor Dimensi Memiliki Panjang
5.Tiga Vektor Dimensi Memiliki Panjang
Panjang vektor yang diwakili oleh tiga komponen matriks adalah:
| (x, y, z) T | = | (X, y, z) T | =  ( x 2 + y 2 + z 2 ) (X 2 + y 2 + z 2)
( x 2 + y 2 + z 2 ) (X 2 + y 2 + z 2)
contoh:
Berapa panjang vektor A (2, -4, 4) T
jawab:
1.(2, -4, 4) T | = ( 2 * 2 + -4 * -4 + 4 * 4) (2 * 2 + -4 * -4 + 4 * 4)
= ( 4+ 16 + 16 ) = (4 + 16 + 16) = 36 = 66.theorema phytagoras
a2 + b2 = c2
contoh: dik: sebuah segitga siku-siku memiliki panjang alas 5cm, dan tingginya 12 cm berapakah panjang sisi miringnya?Jawab: dengan menggunakan konsep phytagoras dapat kita cari bahwa panjang sisi mirngnya adalah:
c2= a2 + b2
=52+122
=25+144
C2 =169
=52+122
=25+144
C2 =169
C=√169
C=13cm, jadi panjang sisi miringnya adalah 13 cm7.rumus sifat assosiatif pada penjumlahan,
(a+b)+c=a+(b+c)
Contoh: (4+4)+6=4+(4+6)
Bukti:8+6=4+10
14 = 14 Terbukti.
8.Rumus ABC
Contoh Soal :Carilah himpunan penyelesaian dari x2 – 2x – 3= 0.
Jawab :
 9.Perkalian vektor dan skalar
9.Perkalian vektor dan skalar Sebelum kita belajar mengenai perkalian vektor, terlebih dahulu kita berkenalan dengan vektor-vektor satuan.
Vektor satuan (unit vektor) merupakan suatu vektor yang besarnya = 1. vektor satuan tidak mempunyai satuan. Vektor satuan berfungsi untuk menunjukan suatu arah dalam ruang. Untuk membedakan vektor satuan dari vektor biasa maka vektor satuan dicetak tebal (untuk tulisan cetak) atau di atas vektor satuan disisipkan tanda ^ (untuk tulisan tangan)
Pada sistem koordinat kartesius (xyz) kita menggunakan vektor satuan i untuk menunjukkan arah sumbu x positif, vektor satuan j untuk menunjukkan arah sumbu y positif, vektor satuan k untuk menunjukkan arah sumbu y positif.
Untuk memudahkan pemahaman dirimu, perhatikan contoh berikut ini. Misalnya terdapat sebuah vektor F sebagaimana tampak pada gambar di bawah.
Pada gambar di atas, tampak bahwa vektor satuan i menunjukkan arah sumbu x positif dan vektor satuan j menunjukkan arah sumbu y positif. Kita dapat menyatakan hubungan antara vektor komponen dan komponenya masing-masing, sebagai berikut :
Fx = Fxi
Fy = Fyj
Kita dapat menulis vektor F dalam komponen-komponennya sebagai berikut :
F = Fxi + Fyj
Misalnya terdapat dua vektor, A dan B pada sistem koordinat xy, di mana kedua vektor ini dinyatakan dalam komponen-komponennya, sebagaimana tampak di bawah :
A = Axi + Ayj
B = Bxi + Byj
Bagaimana jika A dan B dijumlahkan ? gampang…
R = A + B
R = (Axi + Ayj) + (Bxi + Byj)
R = (Ax + Bx)i + (Ay + By)j
R = Rxi + Ryj
Apabila tidak semua vektor berada pada bidang xy maka kita bisa menambahkan vektor satuan k, yang menunjukkan arah sumbu z positif.
A = Axi + Ayj + Azk
B = Bxi + Byj + Bzk
Jika vektor A dan B dijumlahkan maka akan diperoleh hasil sebagai berikut :
R = A + B
R = (Axi + Ayj + Azk) + (Bxi + Byj + Bzk)
R = (Ax + Bx)i + (Ay + By)j + (Az + Bz)k
R = Rxi + Ryj + Rzk
Perkalian titik menggunakan komponen vektor satuan
Kita dapat menghitung perkalian skalar secara langsung jika kita mengetahui komponen x, y dan z dari vektor A dan B (vektor yang diketahui).
Untuk melakukan perkalian titik dengan cara ini, terlebih dahulu kita lakukan perkalian titik dari vektor satuan, setelah itu kita nyatakan vektor A dan B dalam komponen-komponennya, menguraikan perkaliannya dan menggunakan perkalian dari vektor-vektor satuannya.
Vektor satuaj i, j dan k saling tegak lurus satu sama lain, sehingga memudahkan kita dalam perhitungan. Menggunakan persamaan perkalian skalar yang telah diturunkan di atas (A.B = AB cos teta) kita peroleh :
i . i = j . j = k . k = (1)(1) cos 0 = 1
i . j = i . k = j . k = (1)(1) cos 90o = 0
Sekarang kita nyatakan vektor A dan B dalam komponen-komponennya, menguraikan perkaliannya dan menggunakan perkalian dari vektor-vektor satuannya.
A . B = Axi . Bxi + Axi . Byj + Axi . Bzk +
Ayj . Bxi + Ayj . Byj + Ayj . Bzk +
Azk . Bxi + Azk . Byj + Azk . Bzk
A . B = AxBx (i . i) + AxBy (i . j) + Ax Bz (i . k) +
AyBx (j . i) + AyBy (j . j) + AyBz (j . k) +
AzBx (k . i) + AzBy (k . j) + AzBz (k . k)
Bahasa apa’an neh… dipahami perlahan-lahan ya….
Karena i . i = j . j = k . k = 1 dan i . j = i . k = j . k = 0, maka :
A . B = AxBx (1) + AxBy (0) + Ax Bz (0) +
AyBx (0) + AyBy (1) + AyBz (0) +
AzBx (0) + AzBy (0) + AzBz (1)
A . B = AxBx (1) + 0 + 0 +
0 + AyBy (1) + 0 +
0 + 0 + AzBz (1)
A . B = AxBx + AyBy + AzBz
Berdasarkan hasil perhitungan ini, bisa disimpulkan bahwa perkalian skalar atau perkalian titik dari dua vektor adalah jumlah dari perkalian komponen-komponennya yang sejenis.
Gampang khan ? dipahami perlahan-lahan… ntar juga ngerti kok… kaya belajar naek sepeda agar dirimu semakin memahami bahasa alien di atas, mari kita kerjakan latihan soal di bawah ini
Contoh Soal 1 :
Besar vektor A dan B berturut-turut adalah 5 dan 4, sebagaimana tampak pada gambar di bawah. Sudut yang terbentuk adalah 90o. Hitunglah perkalian titik kedua vektor tersebut…
Panduan jawaban :
Sebelum kita menghitung perkalian titik vektor A dan B, terlebih dahulu kita ketahui komponen vektor kedua tersebut.
Ax = (5) cos 0o = (5) (1) = 5
Ay = (5) sin 0o = (5) (0) = 0
Az = 0
Bx = (4) cos 90o = (4) (0) = 0
By = (4) sin 90o = (4) (1) = 1
Bz = 0
Vektor A hanya mempunyai komponen vektor pada sumbu x dan vektor B hanya mempunyai komponen vektor pada sumbu y. Komponen z bernilai nol karena vektor A dan B berada pada bidang xy.
Sekarang kita hitung perkalian titik antara vektor A dan B menggunakan persamaan perkalian titik dengan vektor komponen :
A . B = Ax Bx + AyBy + AzBz
A . B = (5) (0) + (0) (1) + 0
A . B = 0 + 0 + 0
A . B = 0
Masa sich hasilnya nol ?
Coba kita bandingkan dengan cara pertama
A.B = AB cos teta
A.B = (4)(5) cos 90
A.B = (4) (5) (0)
A.B = 0
Hasilnya sama.
Contoh Soal 2 :
Besar vektor A dan B berturut-turut adalah 5 dan 4, sebagaimana tampak pada gambar di bawah. Hitunglah perkalian titik kedua vektor tersebut, jika sudut yang terbentuk adalah 30o
Panduan jawaban :
Sebelum kita menghitung perkalian titik vektor A dan B, terlebih dahulu kita ketahui komponen vektor kedua tersebut.
Komponen z bernilai nol karena vektor A dan B berada pada bidang xy.
Sekarang kita hitung perkalian titik antara vektor A dan B menggunakan persamaan perkalian titik dengan vektor komponen :
Coba kita bandingkan dengan cara pertama.
Hasilnya sama.
Perkalian silang menggunakan komponen vektor satuan
Kita dapat menghitung perkalian silang secara langsung jika kita mengetahui komponen vektor yang diketahui. Urutannya sama dengan perkalian titik.
Pertama-tama, kita lakukan perkalian antara vektor-vektor satuan i, j dan k. Hasil perkalian vektor antara vektor satuan yang sama adalah nol.
i x i = j x j = k x k = 0
Dengan berpedoman pada persamaan perkalian vektor yang telah diturunkan sebelumnya (A x B = AB sin teta) dan sifat anti komutatif dari perkalian vektor (A x B = – B x A), maka kita peroleh :
i x j = -j x i = k
j x k = -k x j = i
k x i = -i x k = j
Sekarang kita nyatakan vektor A dan B dalam komponen-komponennya, menguraikan perkaliannya dan menggunakan perkalian dari vektor-vektor satuannya.
A x B = (Axi + Ayj + Azk) x (Bxi + Byj + Bzk)
A x B = Axi x Bxi + Axi x Byj + Axi x Bzk +
Ayj x Bxi + Ayj x Byj + Ayj x Bzk +
Azk x Bxi + Azk x Byj + Azk x Bzk
A x B = AxBx (i x i) + AxBy (i x j) + Ax Bz (i x k) +
AyBx (j x i) + AyBy (j x j) + AyBz (j x k) +
AzBx (k x i) + AzBy (k x j) + AzBz (k x k)
Karena i x i = j x j = k x k = 0 dan i x j = -j x i = k, j x k = -k x j = i, k x i = -i x k = j, maka :
A x B = AxBx (0) + AxBy (k) + Ax Bz (-j) +
AyBx (-k) + AyBy (0) + AyBz (i) +
AzBx (j) + AzBy (-i) + AzBz (0)
A x B = AxBy (k) + Ax Bz (-j) +
AyBx (-k) + AyBz (i) +
AzBx (j) + AzBy (-i)
A x B = AxBy (k) + Ax Bz (-j) + AyBx (-k) + AyBz (i) + AzBx (j) + AzBy (-i)
A x B = (AyBz - AzBy)i + (AzBx - Ax Bz)j + (AxBy - AyBx )k
Pahami perlahan-lahan….
Jika C = A x B maka komponen-komponen dari C adalah sebagai berikut :
Cx = AyBz - AzBy
Cy = AzBx - Ax Bz
Cz = AxBy - AyBx
10Penyelesaian Persamaan Linear dengan Matriks
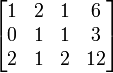 Baris ke 2 dikurangi baris ke 1
Baris ke 2 dikurangi baris ke 1 Baris ke 3 dikurangi 2 kali baris ke 1
Baris ke 3 dikurangi 2 kali baris ke 1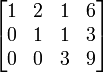 Baris ke 3 ditambah 3 kali baris ke 2
Baris ke 3 ditambah 3 kali baris ke 2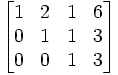 Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris)
Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris)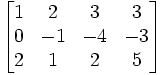 Baris ke 2 dikurangi 2 kali baris ke 1
Baris ke 2 dikurangi 2 kali baris ke 1 Baris ke 3 dikurangi 2 kali baris ke 1
Baris ke 3 dikurangi 2 kali baris ke 1 Baris ke 3 dikurangi 3 kali baris ke 2
Baris ke 3 dikurangi 3 kali baris ke 2 Baris ke 3 dibagi 8 dan baris ke 2 dibagi -1
Baris ke 3 dibagi 8 dan baris ke 2 dibagi -1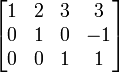 Baris ke 2 dikurangi 4 kali baris ke 3
Baris ke 2 dikurangi 4 kali baris ke 3 Baris ke 1 dikurangi 3 kali baris ke 3
Baris ke 1 dikurangi 3 kali baris ke 3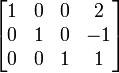 Baris ke 1 dikurangi 2 kali baris ke 2 (Matriks menjadi Eselon-baris tereduksi)
Baris ke 1 dikurangi 2 kali baris ke 2 (Matriks menjadi Eselon-baris tereduksi)
10Penyelesaian Persamaan Linear dengan Matriks
a)Bentuk Eselon-Baris
Matriks dapat dikatakan Eselon-baris apabila memenuhi persyaratan berikut :
- 1.) Di setiap baris, angka pertama selain 0 harus 1 (leading 1).
- 2.) Jika ada baris yang semua elemennya nol, maka harus dikelompokkan di baris akhir dari matriks.
- 3.) Jika ada baris yang leading 1 maka leading 1 di bawahnya, angka 1-nya harus berada lebih kanan dari leading 1 di atasnya.
- 4.) Jika kolom yang memiliki leading 1 angka selain 1 adalah nol maka matriks tersebut disebut Eselon-baris tereduksi
Contoh:
syarat 1: baris pertama disebut dengan leading 1
syarat 2: baris ke-3 dan ke-4 memenuhi syarat 2
syarat 3: baris pertama dan ke-2 memenuhi syarat 3
syarat 4: matriks dibawah ini memenuhi syarat ke 4 dan disebut Eselon-baris tereduksi
b) Operasi Eliminasi Gauss
Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana (ditemukan oleh Carl Friedrich Gauss). Caranya adalah dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang Eselon-baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.
Contoh:
Diketahui persamaan linear : x + 2y + z = 6
x + 3y + 2z = 9
- 2x + y + 2z = 12
Tentukan Nilai x, y dan z
Jawab:
Bentuk persamaan tersebut ke dalam matriks:
Operasikan Matriks tersebut
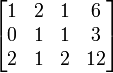 Baris ke 2 dikurangi baris ke 1
Baris ke 2 dikurangi baris ke 1 Baris ke 3 dikurangi 2 kali baris ke 1
Baris ke 3 dikurangi 2 kali baris ke 1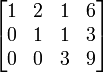 Baris ke 3 ditambah 3 kali baris ke 2
Baris ke 3 ditambah 3 kali baris ke 2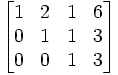 Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris)
Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris)Maka mendapatkan 3 persamaan linier baru yaitu
- x + 2y + z = 6
- y + z = 3
- z = 3
Kemudian lakukan substitusi balik maka didapatkan:
- y + z = 3
- y + 3 = 3
- y = 0
- x + 2y + z = 6
- x + 0 + 3 = 6
- x = 3
Jadi nilai dari x = 3 , y = 0 ,dan z = 3
c) Operasi Eliminasi Gauss-Jordan
Eliminasi Gauss-Jordan adalah pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana. Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris tereduksi. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris tereduksi, maka langsung dapat ditentukan nilai dari variabel-variabelnya tanpa substitusi balik.
Contoh:
Diketahui persamaan linear : x + 2y + 3z = 3
- 2x + 3y + 2z = 3
- 2x + y + 2z = 5
Tentukan Nilai x, y dan z
Jawab:
Bentuk persamaan tersebut ke dalam matriks:
Operasikan Matriks tersebut
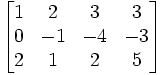 Baris ke 2 dikurangi 2 kali baris ke 1
Baris ke 2 dikurangi 2 kali baris ke 1 Baris ke 3 dikurangi 2 kali baris ke 1
Baris ke 3 dikurangi 2 kali baris ke 1 Baris ke 3 dikurangi 3 kali baris ke 2
Baris ke 3 dikurangi 3 kali baris ke 2 Baris ke 3 dibagi 8 dan baris ke 2 dibagi -1
Baris ke 3 dibagi 8 dan baris ke 2 dibagi -1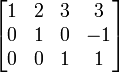 Baris ke 2 dikurangi 4 kali baris ke 3
Baris ke 2 dikurangi 4 kali baris ke 3 Baris ke 1 dikurangi 3 kali baris ke 3
Baris ke 1 dikurangi 3 kali baris ke 3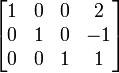 Baris ke 1 dikurangi 2 kali baris ke 2 (Matriks menjadi Eselon-baris tereduksi)
Baris ke 1 dikurangi 2 kali baris ke 2 (Matriks menjadi Eselon-baris tereduksi)Maka didapatkan nilai dari x = 2 , y = − 1 ,dan z = 1
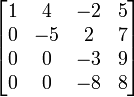

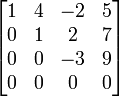




Tidak ada komentar:
Posting Komentar